by Theresa L. Ford
Printable .PDF Version
Cattail.Nu
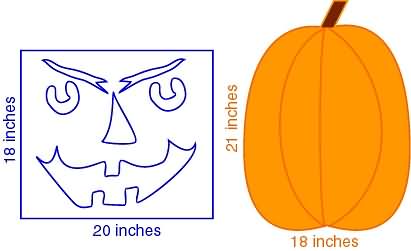
Here's the pumpkin carving pattern we bought:

Here's the best pumpkin from the patch:
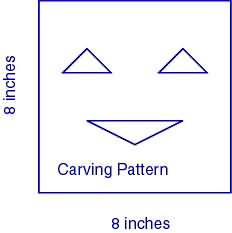
Notice we have an obvious problem!
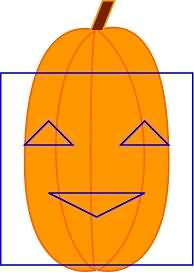
That's right! His eyes are entirely too far apart and his mouth is too close to his eyes. We don't want a fish-eyed pumpkin, so we must correct the pattern. We'll use math to save the pumpkin's face!
First, let's find the change (translation) that must be made. Here's two lines (ahem! linear functions) we'll use to determine the translation equation. We'll pretend all our lines go off to infinity.
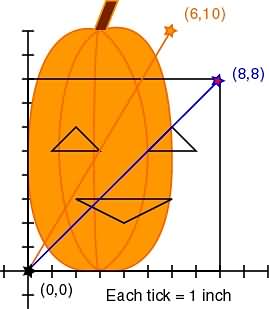
The pattern line is a graph of y=x.
The pumpkin line is a graph of y=(5/3)x.
These can be found by using the points on the line
to put the equations in slope-intercept form (y = mx + b).
(8,8) and (0,0) are points on the pattern line. slope m = change in y / change in x y intercept b = 0 (line cuts through the origin) m = (8-0) / (8-0) = 8/8 = 1 So: y = 1x + 0 y = x (6,10) and (0,0) are points on the pumpkin line. y intercept b = 0 (line cuts through the origin) slope m = change in y / change in x m = (10-0) / (6-0) = 10/6 = 5/3 So: y = (5/3)x + 0 y = (5/3)x
But the exact equations of the lines aren't really important and can now be mostly forgotten. We need to find out how much to stretch and shrink the pattern line to get the pumpkin line.
Quick Review: Vertical and Horizontal Shrink/Stretch of Linear Functions
Linear function: y = x
Translations:
y = af(cx)
c is the horizontal squish: 0<c<1 wider
c>1 narrower
a is the vertical squish: 0<a<1 shorter
a>1 taller
Old points in the function (x, y)
New points in the function ((x/c), ya)
Using the original point (x,y) and new point (x/c, ya), we can solve for c and a to create the formula h(x)=af(cx) which can stretch and shrink vertically and horizontally the pattern line (function y=x). Luckily, both lines go through (0,0) so we don't have to worry about left or right shifting (or up or down).
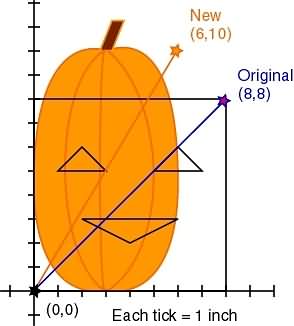
For original point (8,8) and new point (6,10):
Each x is divided by c to get the new x
Each y is multiplied by a to get the new y
new x = original x / c
6 = 8/c
6c = 8
c = 8/6
c = 4/3
new y = original ya
10 = 8a
10/8 = a
5/4 = a
So our equation of change (translation) is: y = (5/4)*((4/3)x)
Check:
y = (5/4)*((4/3)x) = ((5/4)*(4/3))x = (5/3)x
We should be able to reach our pumpkin line by stretching y=x vertically using
y = (5/3)x (thus a = 5/3 for the new equation)
(Pretend you didn't notice this is the same
answer we got using the slope formula above)
x = 8
new y = original ya
y = 8(5/3) = 40/3 = 13.3
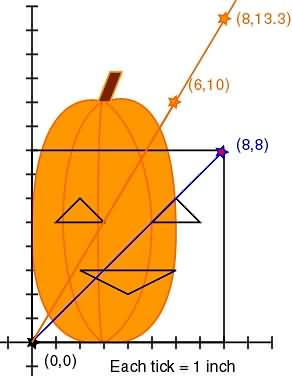
We definitely have our translation correct, so now we can apply it to other lines (linear functions). We'll keep using the unsimplified version so we get the same proportionate distance from the origin when we squish the linear functions.
y = a * ( c )x y = (5/4)*((4/3)x) Original points in the functions (x, y) New points in the functions ((x/c), ya)
We'll create some more linear functions (lines) to squish by connecting some of our points back to the origin (0,0).
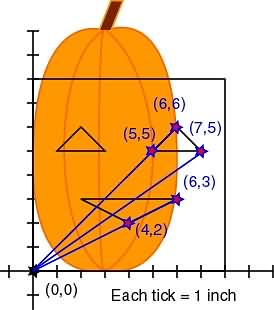
Now it's a simple matter of applying our translation to all the linear functions using the points. Technically, we're multiplying the stretch/shrink times the line equations for each of these points, but we're skipping the part where we actually care about what the function of each line is. We don't even really care about the resulting function equations, either. We're just looking at the points ON the function graphs. Just keep in mind that we're squishing (stretching and shrinking) linear functions, not just moving points around.
Translation Summary: a = 5/4 c = 4/3 y = a * ( c )x y = (5/4)*((4/3)x) Original points in the functions (x, y) New points in the new functions ((x/c), ya)
Top Eye Point:
Original (6,6)
a = 5/4
c = 4/3
New ( x , y )
( (x/c) , ya )
( 6/(4/3) , 6* (5/4) )
( 18/4 , 30/4 )
( 4 1/2 , 7 1/2 )
| |
Bottom Left of Eye:
Original (5,5)
a = 5/4
c = 4/3
New ( x , y )
( (x/c) , ya )
( 5/(4/3) , 5* (5/4) )
( 15/4 , 25/4 )
( 3 3/4 , 6 1/4 )
|
Bottom Right of Eye:
Original (7,5)
a = 5/4
c = 4/3
New ( x , y )
( (x/c) , ya )
( 7/(4/3) , 5* (5/4) )
( 21/4 , 25/4 )
( 5 1/4 , 6 1/4 )
|
Bottom of Mouth:
Original (4,2)
a = 5/4
c = 4/3
New ( x , y )
( (x/c) , ya )
( 4/(4/3) , 2* (5/4) )
( 12/4 , 10/4 )
( 3 , 2 1/2 )
|
Top Right of Mouth:
Original (6,3)
a = 5/4
c = 4/3
New ( x , y )
( (x/c) , ya )
( 6/(4/3) , 3* (5/4) )
( 18/4 , 15/4 )
( 4 1/2 , 3 3/4 )
|
I know you didn't actually read all those equations (I tried not to and I was writing them). Let's just look at the pretty picture.
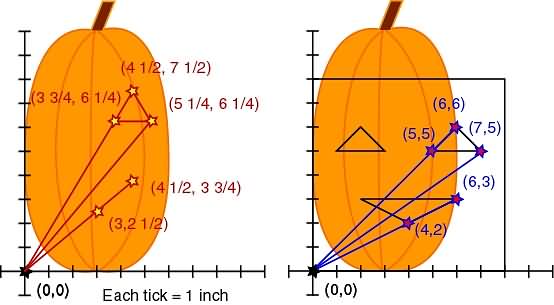
Hey! That's looking pretty good! Who would have thought you could stretch and shrink linear functions to redesign a pumpkin pattern? Now... What about all those other points? Like the other eye? Who wants a one-eyed pumpkin with half a mouth?
Let's avoid more stretching and shrinking of lines and play with reflections. Luckily our pattern reflects across the y axis. Well, it will once we move it over!
We'll shift all those lines over to the left 3 units.
We're picking 3 because that's half the width of our pumpkin.
That would take our original pattern line (y=x)
and make it y=x+3
and our original pumpkin line (y=(5/3)x)
into y=(5/3)x+5.
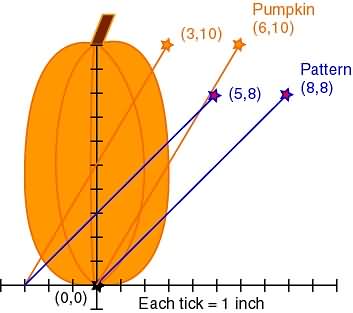
Wait. We just subtracted 3 from all the x values and we are saying the equations are adjusted by + 3 and + 5? What?! OH! The y-intercepts changed to (0,3) and (0,5), respectively. We're moving lines around.
We can look at the pattern equation shift two ways. y=x+3 can be shift up 3 OR shift left 3. If we moved it up by 3, moving (8,8) to (8,11), the line gets extended out to the x-axis. We just pick our new point as the point on the new line that is horizontal from our original point. We're not that dedicated, though, so we'll simply read y=x+3 as "shift left 3".
Our pumpkin line was a bit more complicated. We actually shift it left by y=(5/3)(x+3), which equals (5/3)x + (5/3)3 and then (5/3)x+5. Easier to just look at the y-intercept on the graph, isn't it?

We really don't need those original lines. Let's forget about them and shift all the other, more interesting, lines left 3.
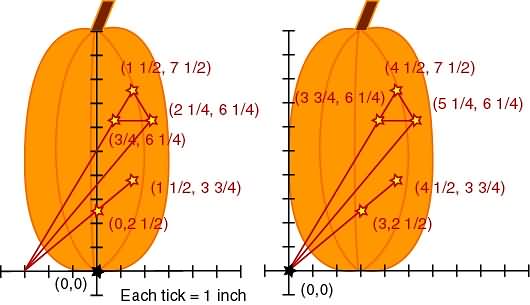
We remember that reflections across the y-axis merely change the x value to -x, so let's reflect!
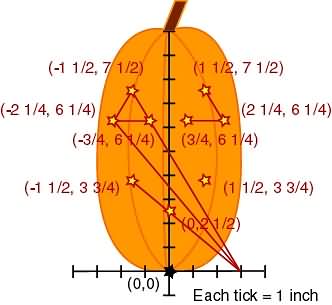
And we learned how to connect the dots in kindergarten.
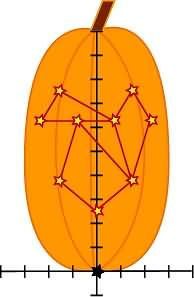
Some of us did... Others of us are still struggling with the basics.
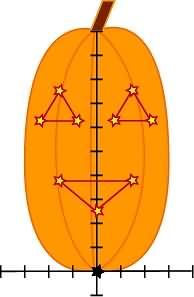
Now we have our new pattern that is perfectly proportional to our original pattern.
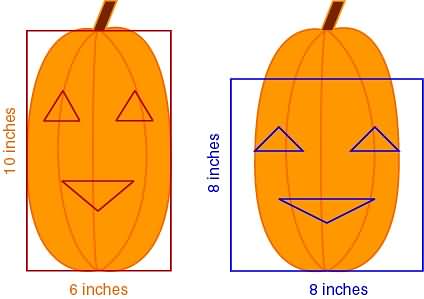
Of course there are other, easier ways to do this same thing, but that wasn't the point, now was it?! It's supposed to be SCARY Halloween Math. Are you scared yet? No? Good! Here's a pumpkin and a pattern for you to try out your math skills: